3DoFの動作となります。
このパノラマ画像を使用したVR空間上で特定の方向に移動できるようにし、
また、極力負荷をかけない計算を行い、制限付きの6DoF操作ができるようにします。
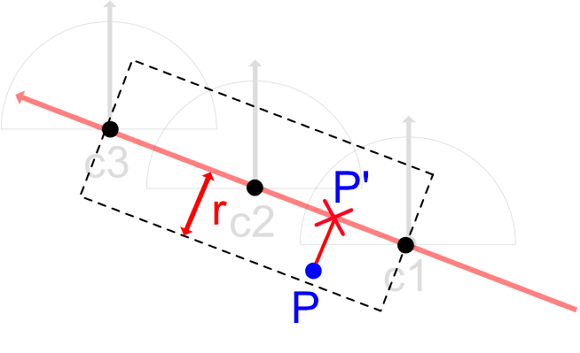
※ ここでは、半球の180度パノラマで視差を考慮したステレオ情報を持つ状態を"180度パノラマ-3D"と呼ぶことにします。

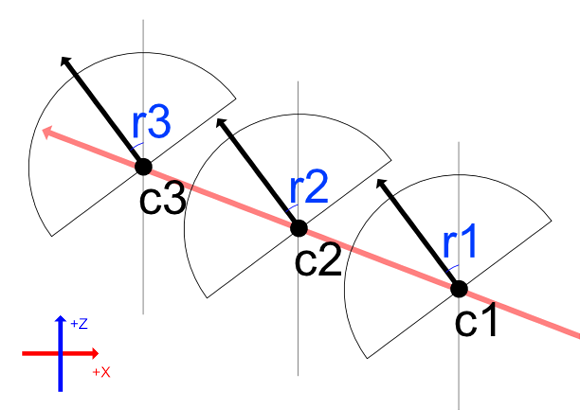
なお、ここでは座標系をUnityでの左手系(スクリーンの右向きに+X、スクリーンの上向きに+Y、スクリーンの前方に+Z)で説明していきます。



depth = (zDist < farPlane) ? ((zDist - nearPlane) / zDist) : 1.0;
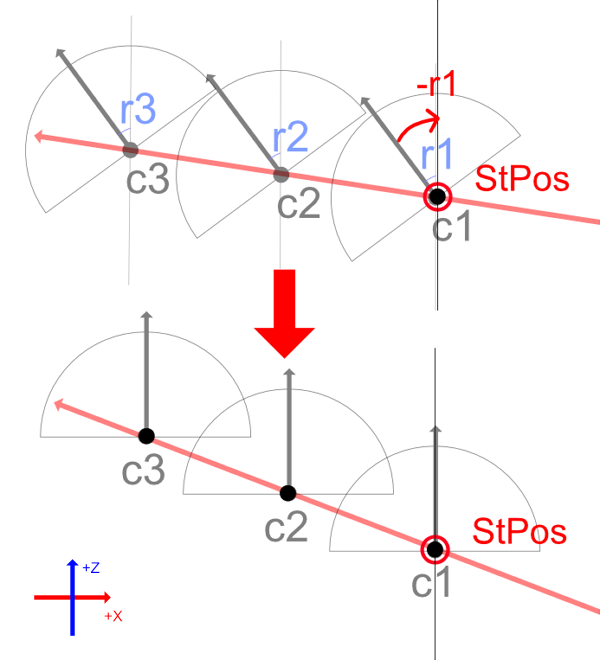
// Y軸中心に-r1度回転する行列.
Matrix4x4 rotYMat = Matrix4x4.Rotate(Quaternion.Euler(0.0f, -r1, 0.0f));
// カメラ位置を変換.
Vector3 basePos = c1;
c1 = rotYMat.MultiplyVector(c1 - basePos) + StPos;
c2 = rotYMat.MultiplyVector(c2 - basePos) + StPos;
c3 = rotYMat.MultiplyVector(c3 - basePos) + StPos;



float4 col1 = tex2D(_Tex1, uv); // カメラc1でのテクスチャ_Tex1での指定のUVでの色を取得.
float4 col2 = tex2D(_Tex2, uv); // カメラc2でのテクスチャ_Tex2での指定のUVでの色を取得.
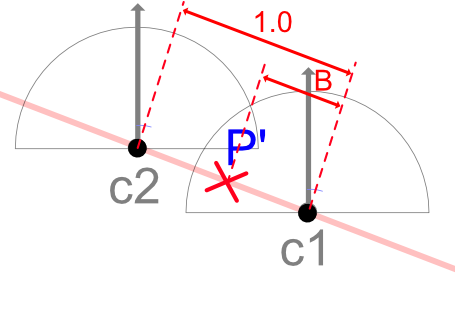
float4 col = lerp(col1, col2, B); // ブレンド値B(0.0 - 1.0)により合成.
float3 calcVDir (float2 _uv) {
float theta = UNITY_PI2 * (_uv.x - 0.5);
float phi = UNITY_PI * (_uv.y - 0.5);
float sinP = sin(phi);
float cosP = cos(phi);
float sinT = sin(theta);
float cosT = cos(theta);
float3 vDir = float3(cosP * sinT, sinP, cosP * cosT);
return vDir;
}
float2 calcWPosToUV (float3 wPos, float3 centerPos) {
float3 vDir = normalize(wPos - centerPos);
float sinP = vDir.y;
float phi = asin(sinP); // from -π/2 to +π/2 (-90 to +90 degrees).
float cosP = cos(phi);
if (abs(cosP) < 1e-5) cosP = 1e-5;
float sinT = vDir.x / cosP;
float cosT = vDir.z / cosP;
sinT = max(sinT, -1.0);
sinT = min(sinT, 1.0);
cosT = max(cosT, -1.0);
cosT = min(cosT, 1.0);
float a_s = asin(sinT);
float a_c = acos(cosT);
float theta = (a_s >= 0.0) ? a_c : (UNITY_PI2 - a_c);
float2 uv = float2((theta / UNITY_PI2) + 0.5, (phi / UNITY_PI) + 0.5);
if (uv.x < 0.0) uv.x += 1.0;
if (uv.x > 1.0) uv.x -= 1.0;
return uv;
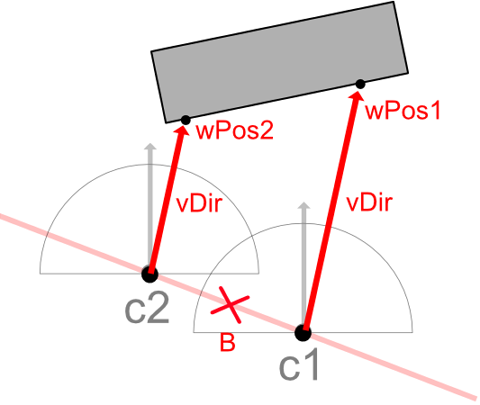
}float depth1 = tex2D(_TexDepth1, uv).r;
float depth2 = tex2D(_TexDepth2, uv).r;float zDist1 = (depth1 >= 0.99999) ? farPlane : (nearPlane / (1.0 - depth1));
float zDist2 = (depth2 >= 0.99999) ? farPlane : (nearPlane / (1.0 - depth2));float3 wPos1 = (vDir * zDist1) + c1;
float3 wPos2 = (vDir * zDist2) + c2;
/**
* UV位置と方向ベクトルより、衝突するワールド座標位置を計算.
* @param[in] depthTex depthテクスチャ.
* @param[in] uv UV値.
* @param[in] cPos カメラのワールド座標での中心.
* @param[in] vDir 視線ベクトル.
*/
float3 calcUVToWorldPos (sampler2D depthTex, float2 uv, float3 cPos, float3 vDir) {
float depth = tex2D(depthTex, uv).r;
// depth値から、カメラからの距離に変換.
depth = (depth >= 0.99999) ? farPlane : (nearPlane / (1.0 - depth));
depth = min(depth, farPlane);
// 衝突したワールド座標位置.
return (vDir * depth) + cPos;
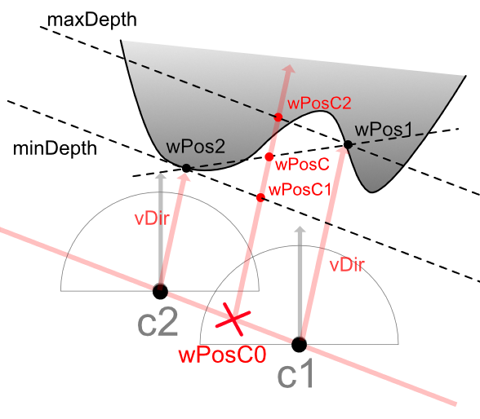
}float3 wPosC = lerp(wPos1, wPos2, B);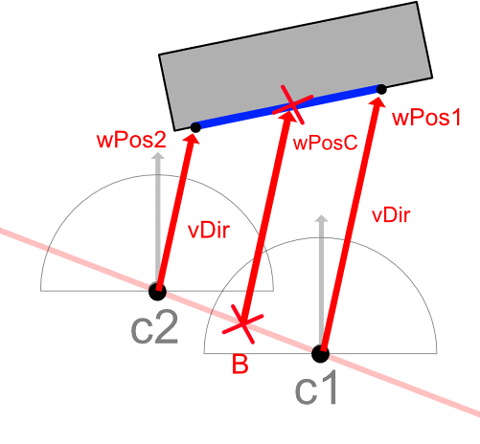
float3 wPosC0 = lerp(c1, c2, B); // c1-c2直線上のBのワールド位置.
// ワールド座標でのwPosCを、c1のカメラでのUV値に変換.
float2 newUV1 = calcWPosToUV(wPosC, c1);
// ワールド座標でのwPosCを、c2のカメラでのUV値に変換.
float2 newUV2 = calcWPosToUV(wPosC, c2);
// UV値より、それぞれのワールド座標位置を計算.
float3 wPosA = calcUVToWorldPos(_TexDepth1, newUV1, c1, normalize(wPosC - c1));
float3 wPosB = calcUVToWorldPos(_TexDepth2, newUV2, c2, normalize(wPosC - c2));
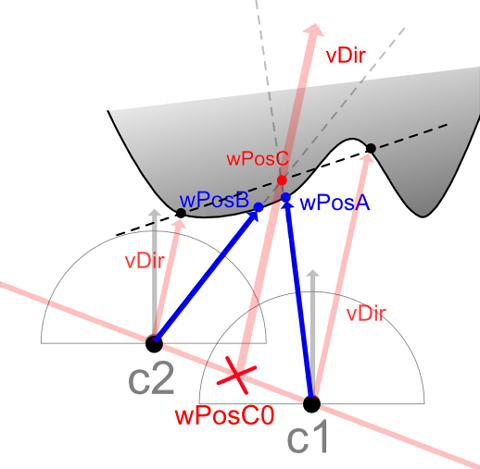
float angle1 = dot(normalize(wPosA - wPosC0), vDir);
float angle2 = dot(normalize(wPosB - wPosC0), vDir);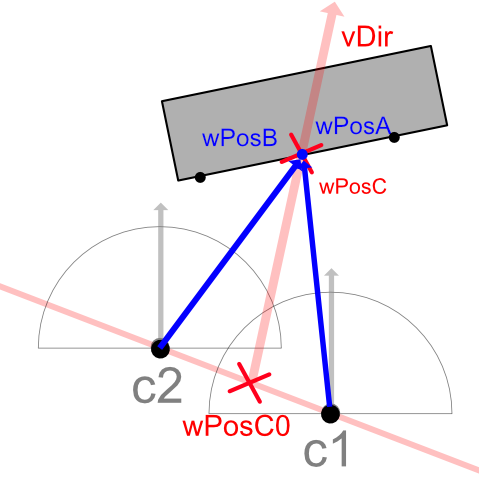
// c1でのRGBテクスチャを_Tex1、c2でのRGBテクスチャを_Tex2とする.
// 計算されたUVより、ピクセル色を取得.
float4 col1 = tex2D(_Tex1, newUV1);
float4 col2 = tex2D(_Tex2, newUV2);
float4 col = float4(0, 0, 0, 1);
if (angle1 > 0.99999 && angle2 > 0.99999) {
col = lerp(col1, col2, B);
}
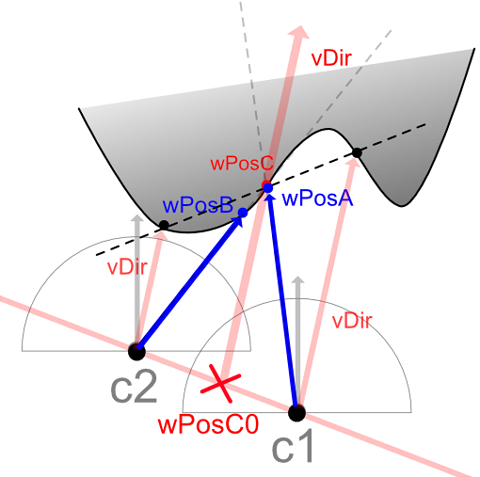
// 計算されたUVより、ピクセル色を取得.
float4 col1 = tex2D(_Tex1, newUV1);
float4 col2 = tex2D(_Tex2, newUV2);
float4 col = float4(0, 0, 0, 1);
if (angle1 > 0.99999 && angle2 <= 0.99999) {
col = col1;
} else if (angle2 > 0.99999 && angle1 <= 0.99999) {
col = col2;
}